Conic Sections Rotation Of Axes

To eliminate this term you can use a procedure called rotation of axes.

Conic sections rotation of axes. If either latex a latex or latex c latex is zero then the graph may be a parabola. Notice the phrase may be in the definitions. If the value of is zero then the conic is not rotated and sits on the x and y axes.

As we have seen conic sections are formed when a plane intersects two right circular cones aligned tip to tip and extending infinitely far in opposite directions which we also call a cone. As we have seen conic sections are formed when a plane intersects two right circular cones aligned tip to tip and extending infinitely far in opposite directions which we also call a cone. If b 0 the conic section will have a vertical and or horizontal axes.

That is because the equation may not represent a conic section at all depending on the values of a b c d e and f. If b does not equal 0 as shown below the conic section is rotated. Write equations of rotated conics in standard form.

Write equations of rotated conics in standard form. Notice the phrase may be in the definitions. Graphing graphing a rotated conic.

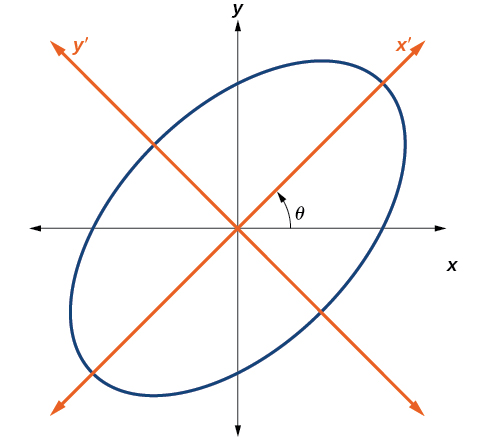
If is non zero then the conic is rotated about the axes with the rotation centred on the origin. The new second degree equation of the conic after the axes have been rotated will look like this. Instead of using the xy plane the conic can be expressed as a second degree equation ax 2 cy 2 dx ey f 0 in the x y plane.

Notice the phrase may be in the definitions. The objective is to rotate the and axes until they are parallel to the axes of the conic. We saw in section 5 2 that the graph of the quadratic equation ax2 cy2 dx ey f 0 is a parabola when a 0orc 0 that is when ac 0.