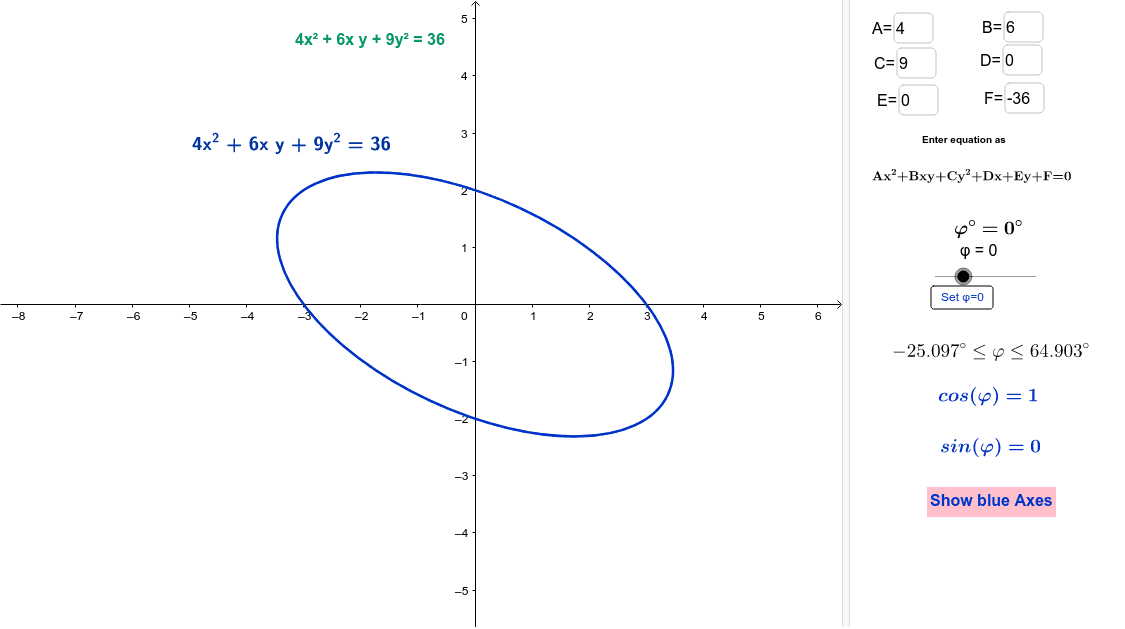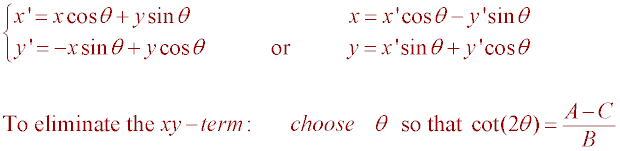Rotating Conic Sections

Rotation of axes 1 rotation of axes at the beginning of chapter 5 we stated that all equations of the form ax2 bxy cy2 dx ey f 0 represented a conic section which might possibly be degenerate.

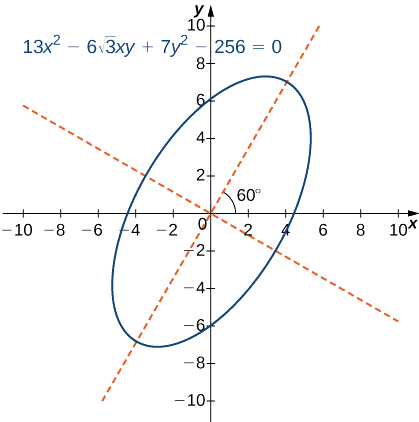
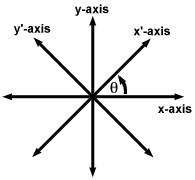
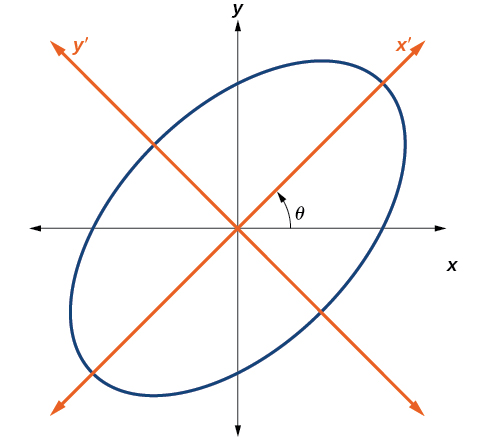
Rotating conic sections. By the end of this section you will be able to. How do i rotate the axes of and then graph 7x 2 6sqrt3xy 13y 2 16 0. When a conic contains an xy term the x and y axes can be rotated through an angle of θ such that they are once again parallel with the axes of the conic thus eliminating the xy term of the conic.

Conic sections are important in astronomy. Identify conics without rotating axes. Conic sections calculator calculate area circumferences diameters and radius for circles and ellipses parabolas and hyperbolas step by step.

The general equation for such conics contains an term. The orbits of two massive objects that interact according to newton s law of universal gravitation are conic sections if their common center of mass is considered to be at rest. The standard form of the conic section is the equation below.

If they are moving apart they will both follow parabolas or hyperbolas. . A rotation of the coordinate axes looks something like this.

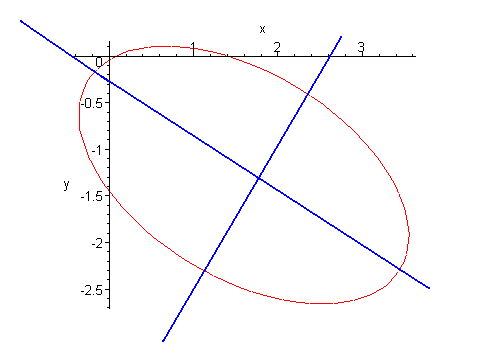
How to rotate conic sections using quadratic forms. In this section you will study the equations of conics whose axes are rotated so that they are not parallel to either the axis or the axis. To eliminate this term you can use a procedure called rotation of axes.

Writing equations of rotated conics in standard form now that we can find the standard form of a conic when we are given an angle of rotation we will learn how to transform the equation of a conic given in the form displaystyle a x 2 bxy c y 2 dx ey f 0 ax 2. In section 5 3 we found that. We saw in section 5 2 that the graph of the quadratic equation ax2 cy2 dx ey f 0 is a parabola when a 0orc 0 that is when ac 0.